Circle theorems: equal length tangents

1. Thales. The easiest circle theorem.
2. Inscribed angle. The angle subtending a major arc is constant.
3. Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
4. Tangent radius. Blindingly obvious, but a slippery proof.
5. Alternate segment. Perhaps the most unintuitive.
6. Chord bisection by radius. The relevant angle is 90°.
7. Equal length tangents. For completeness.

Statement

If lines extended from a point P meet a circle tangentially at points A and B then |PA| = |PB|.

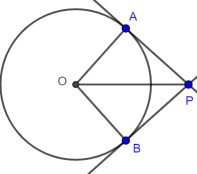
As is often the case in stating theorems, brevity and precision conflict; a statement such as "tangents which meet at the same point are equal in length" is brief but somewhat misleading: tangents can extend beyond A and B, meet at the same point (P), but still differ in length.

Proof

The tangent radius theorem implies that the radii OA and OB make an angle of 90° with the tangents.

ΔPAO is right angled so, by Pythagoras, |PA|² = |PO|² - |OA|². Similarly, |PB|² = |PO|² - |OB|².

Subtracting, |PA|² - |PB|² = |OB|² - |OA|² = 0, as OA and OB are both radii. So |PA|² = |PB|² and |PA| = |PB|. ∎

The Math open reference site has a rather nice tangent construction with proof that they are indeed tangents.

Where next?

Oxford’s latest maths annual newsletter has just dropped into my inbox. Its postscript observes that:

1. The year 20-21 concatenates two consecutive integers, as does 21-22, 22-23 …. 100-101 etc.
2. 2021 is the product of two primes, 43 and 47. The last such year was 1763. The next will be 2491.

So far, so easy. The next time (1) and (2) will occur in a year will apparently be 794018604377235322848433897872605582794018604377235322848433897872605583.

According to numbersaplenty.com Oxford’s “next occurrence” claim is wrong, as 2307340946901148-2307340946901147 is the product of the primes 4803478892324963 and 4803478892324969.

I have yet to check these! We need restricted solutions of \( p_1p_2 = (10^{dig(n)}+1)n + 1 \) where \( n \) has \( dig(n) \) digits.

(Having used Geogebra for these circle theorems, I just squeezed in Katex).

As Ramanujan might have said, 2021 seems interesting year.