Circle theorems: tangent radius
- Thales. The easiest circle theorem.
- Inscribed angle. The angle subtending a major arc is constant.
- Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
- Tangent radius. Blindingly obvious, but a slippery proof.
- Alternate segment. Perhaps the most unintuitive.
- Chord bisection by radius. The relevant angle is 90°.
- Equal length tangents. For completeness.
Statement
The angle between a circle’s radius and the tangent at its end is 90°.
This is my least favourite circle theorem. While the result seems clear discussions suggest people find it hard to prove or disagree over what is an acceptable proof.
This and the risk of diagram dependency this is largely what put me off geometry years ago. Let’s take a careful look.
A simple fully constructive proof
Draw a diameter AB and construct a perpendicular diameter PQ, using the standard perpendicular bisector construction. Construct a line A’B’ parallel to AB through Q using this neat method.
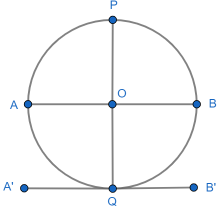
AB and A’B’ are parallel, so |AA| = |B’B’| = |OQ|. All points on BQA, other than Q, have distance to AB of less than |OQ|.
Therefore A’B’ intersects the circle at precisely one point, Q, and so is (by definition) a tangent at Q. As AB and A’B’ are parallel, ∠B’QO’ = ∠BOP = 90°. ∎
Does the proof need to be constructive? I think not: for me the line A’B’ with the required characteristics clearly exists. But an awkward person might want more!
I like the minimalist reflection proof mentioned later even more.
An alternative proof
In the diagram below the chord bisection theorem says that if the radius OQ bisects the chord AB then ∠OCA = ∠OCB = 90°.
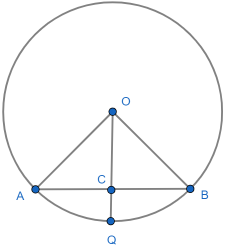
Draw a line parallel to AB through Q. We can do this in several ways, just using ruler and straight edge. A neat way uses similar triangles. Extend OA to A’ and OB to B’ to meet this parallel line:
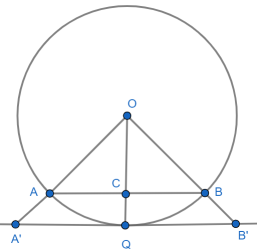
Since A’B’ is parallel to AB the common distance between the two lines is |CQ|. All the points on the arc AQB, other than the point Q, are closer to AB than |CQ|. So A’B’ intersects the circle at precisely one point, Q, and so is (by definition) a tangent at Q.
Finally since we already know that ∠OCB = 90° and A’B’ is parallel to AB, ∠OQB’ = 90°. ∎
This proof aims to rigorously extend the chord bisection theorem but my approach above uses the same idea, but more simply. It also removes the dependency on the chord bisection theorem.
Is the result obvious?
Are there other reasons we might think the result obvious? Look again at the diagram:

A direct extension of the chord bisection theorem suggests ∠OQB’ is clearly 90° though a picky person might say the chord has disappeared at that point.
Minimalist reflection. Suppose ∠OQA’ = α and ∠OQB’ = β. Reflect the diagram in OQ. Everything is the same, as AB was horizontal and A’B’ was parallel to AB. α and β swap, so that α = β. Clearly α + β = 180°, so we have α = β = 90°.
The last one is my personal favourite: it uses the circle, radius and tangent symmetry and captures the "obvious" nature of the result. Is it sufficiently rigorous?
Where next?
Next is the alternate segment theorem.
Also check out these outstanding construction worksheets. These construction techniques seem to have faded from maths education.