Circle theorems: chord bisection

  1. Thales. The easiest circle theorem.
  2. Inscribed angle. The angle subtending a major arc is constant.
  3. Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
  4. Tangent radius. Blindingly obvious, but a slippery proof.
  5. Alternate segment. Perhaps the most unintuitive.
  6. Chord bisection by radius. The relevant angle is 90°.
  7. Equal length tangents. For completeness.

Chord bisection by radius theorem

If a chord AB is bisected at C by a radius OD then ∠OCQ = 90°. This is a simple and intuitively obvious. The set up is:

chord bisection

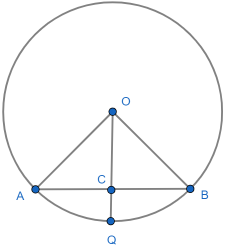
The proof

In the diagram we aim to show that ΔOAC and ΔOBC are congruent, so have the same angles.

In ΔAOC and Δ:

  1. Since both are radii, |OA| =|OB|.
  2. OC is a common side.
  3. |AC| = |BC| as OQ bisects AB.

By the SSS theorem - which most allow you to take as axiomatic - we conclude that that the two triangles are congruent. In particular ∠ACO = ∠BCO. But it is also clear that ∠ACO + ∠BCO = 180° so we conclude that ∠BCO = 90°, as required.

Where next?

Finally we have a theorem about equal length tangents.