Circle theorems: inscribed angle

  1. Thales. The easiest circle theorem.
  2. Inscribed angle. The angle subtending a major arc is constant.
  3. Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
  4. Tangent radius. Blindingly obvious, but a slippery proof.
  5. Alternate segment. Perhaps the most unintuitive.
  6. Chord bisection by radius. The relevant angle is 90°.
  7. Equal length tangents. For completeness.

Thales’s theorem is that the angle made between points A and B on the ends of a circle diameter and a third point P on the circle circumference is 90°.

If we move beyond Thales, so that the points A and B are on the circumference but do not form a diameter, the corresponding theorems become more interesting - and more challenging to prove.

The inscribed angle theorem can be stated in several ways. My preference is that “the angle on the circumference of the major arc is half that at the centre”.

Try it yourself

In the diagram below you can move all the points except O, the centre of the circle. This helps us makes sense of what the theorem is saying and also points to two other related results.

First try moving around the point P. Without moving A, O or B, move P between A and B: ∠APB stays at 45°.

As an aside, ∠AQB is 135° i.e. 180° minus ∠APB. We’ll see more of this later.

Now move around the point A between P and Q. The angles change, but we still have:

Finally move around the point Q between A and B. We have:

If P lies between A and B on the major arc and similarly for Q in the minor arc, we have three results:

  1. Major arc: ∠APB is constant and is equal to half of ∠AOB.
  2. Cyclic quadrilateral: ∠APB+∠AQB=180°.
  3. Minor arc: ∠AQB is constant and is equal to 180° minus half of ∠AOB.

We will now prove 1, while leaving 2 and 3 until our cyclic quadrilaterals article.

Proof: angle on major arc

We break the result into three parts.

In the first part we have a diagram where the centre of the circle, O, lies within ΔAPB. In this case we draw the (red) line OP. AO and OP are radii, so are the same length.

This means ΔAOP is isosceles, so we can call the two equal angles α, as shown. Similarly in ΔBOP we have equal angles β.

inscribed angle proof part 1

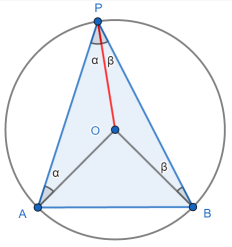
Since the angles in a triangle sum to 180° we must have ∠AOP = 180°-2α. Similarly ∠BOP = 180°-2β.

It is also clear that the three angles surrounding O total 360° so that 360° = ∠AOP + ∠BOP + ∠AOB.

Substituting what we know, we have 360° = 180°-2α + 180°-2β + ∠AOB.

This simplifies to ∠AOB = 2(α + β).

From this follows two things:

  1. The angle at the centre is twice the angle at the circumference.
  2. ∠APB is constant. ∠AOB = 2(α + β) is independent of P. So α + β is constant.

The proof often stops there - for example see this flawed proof from BBC bitesize.

Great. Job done, right? Not quite. One important point with geometry problems like this ... is that we have to make sure that our arguments work whatever the diagram.

Source: mathematician Vicky Neale

The proof is incomplete, falling victim to diagram dependency - in this case choosing a “convenient” diagram in the set up. As soon as we move P far enough left (or right) the partial pretty proof falls apart. This is also confirmed by this wikipedia article.

In the second part we move P further to the left, so that BOP is a straight line. The previous argument will not work.

inscribed angle proof part 2

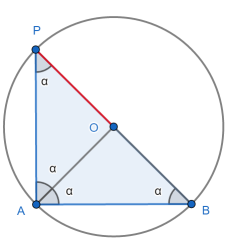
We use Thales’s theorem: ∠BAP = 90°, so that α = 45°. As it is also clear that ∠AOB = 90° we have ∠APB = ∠AOB /2.

Alternatively we note that the total angles in ΔBAP is 4α = 180° so, again, α = 45°.

In the third part we move P further still to the left (or to the right) so that the centre O lies outside of ΔAPB.

Inscribed angle proof part 3

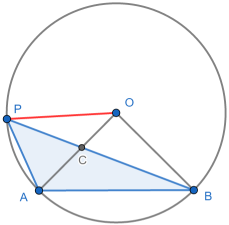
Again we want to show that ∠APB = ∠AOB / 2 = α, say. We again draw the red radius. As OP and OB are both radii, ΔBOP is isosceles, so we can fill in the angles β.

As OP and OA are both radii, ΔAOP is isosceles, so we can fill in the ∠OAP = α + β. We’ve got to here:

inscribed angle proof part 3

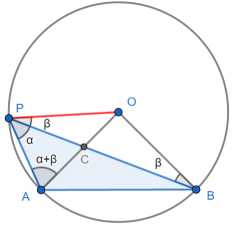
We now have a so-called “angle chase”:

So ∠APB = ∠AOB / 2 = α in this third case.

That’s all three cases proved. ∎

Where next?

For the minor arc and opposite angles results see cyclic quadrilaterals.