Circle theorems: cyclic quadrilateral opposite angles
- Thales. The easiest circle theorem.
- Inscribed angle. The angle subtending a major arc is constant.
- Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
- Tangent radius. Blindingly obvious, but a slippery proof.
- Alternate segment. Perhaps the most unintuitive.
- Chord bisection by radius. The relevant angle is 90°.
- Equal length tangents. For completeness.
Cyclic quadrilateral definition
A cyclic quadrilateral is one whose four vertices can be placed on the circumference of a circle. Not all quadrilaterals are cyclic.
Two results
- Opposite angles of a cyclic quadrilateral sum to 180°.
- On the minor arc ∠BQA is constant.
From the inscribed angle theorem the angle a chord makes with a point on its major arc is constant. Putting this together with (1) leads immediately to (2).
Try it yourself
We’ve seen this diagram before - for the inscribed angle theorem, where the point Q is not usually drawn. But here it allows us to draw a cyclic quadrilateral.
In the diagram below you can move around any point except O.
Before we do this, let’s think about the set up, to ensure we don’t fall into a diagram dependency trap.
Four points on a circle might appear to be awkwardly placed: perhaps all fall one side of a diameter. But in any situation we can draw a line between the first and third points, A and B, rotating the diagram so that the AB chord is horizontal.
We now have P on the major arc and Q on the minor arc. We do not know the length of AB, the exact positioning of P or Q or the angles ∠APB or ∠AQB.
But just have a play. Move A and B around until you’re happy. Then keep A and B fixed and move P and/or Q. Note that:
- ∠APB is constant, as expected from the inscribed angle theorem.
- ∠APB + ∠AQB = 180°.
- ∠AQB is constant.
A misleading traditional proof?
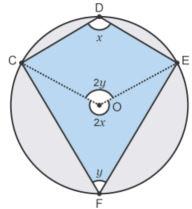
The proof at BBC bitesize - essentially summarized to the left - seems misleading. It assumes the constant angle on a minor arc result, but they have proved only the major arc result.
The problem is that the x and 2x parts have not been justified, nor is it obvious why we can assume that O is inside ΔCEF.
Our proof is quite different.
The quadrilateral proof
This is my own proof, though it would be a surprise if it existed nowhere else.
From the inscribed angle theorem we know that ∠APB is constant (= α say) as P varies over the major arc. For any given Q this means that ∠APB + ∠AQB is constant as P varies over the major arc.
This means that we are allowed to choose P conveniently. This is a rather neat reversal of my normal diagram dependency proof critique.
We choose P so that O lies within the ΔAPB. We draw additional radii OP and OQ. We then have four isosceles triangles. We set their equal angles α, β, γ, and δ as shown.
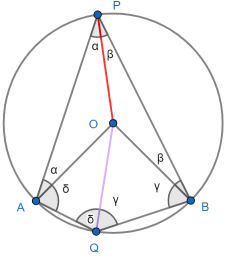
The sum of the angles in the four triangles is also the sum of the labelled angles plus those around the centre of the circle. So 4*180° = 360° + 2(α + β + γ + δ).
Rearranging, we have 180° = (α + β) + (γ + δ) = ∠APB + ∠AQB, as required. ∎
The angle on minor arc proof
We knew that on the major arc ∠APB is constant. We now know that ∠APB + ∠AQB is constant and equal to 180°. We deduce that on the minor arc ∠AQB is constant and is equal to 180° - ∠APB.
Where next?
After all that excitement it’s time for the technical tangent radius theorem.