Circle theorems: alternate segment

1. Thales. The easiest circle theorem.
2. Inscribed angle. The angle subtending a major arc is constant.
3. Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
4. Tangent radius. Blindingly obvious, but a slippery proof.
5. Alternate segment. Perhaps the most unintuitive.
6. Chord bisection by radius. The relevant angle is 90°.
7. Equal length tangents. For completeness.

Statement and diagram

The alternate segment theorem states that the angle between the tangent and chord equals the angle in the alternate segment. The alternate segment? A diagram can help unpack that.

Let’s draw:

• a circle, centre O
• a point P on its circumference
• a tangent to the circle at P

Now connect:

• O and P to form a radius
• P, A and B to form a triangle

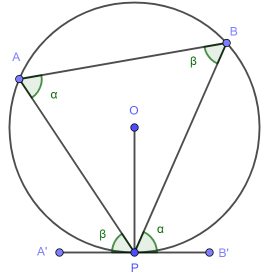
The chord PA divides the circle into a major segment and a minor segment. There is an angle in each and the alternate segment theorem says these are equal - in our diagram to β.

Similarly, the chord PB divides the circle into major minor segments and the highlighted angles are equal - to α, say.

The “most opposite” angles are equal.

Important notes to the diagram

The diagram is usually drawn as above but in general:

• the circle centre O does not have to be inside ΔPAB
• the point P does not have to be on the major segment

We can therefore pull A and B down, so that neither of the above hold and the angle equivalence will remain, although the values of α and β will of course change.

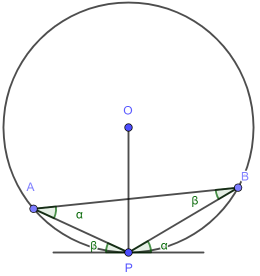
Try it yourself

This is perhaps the least intuitive of the circle theorems. Have a play!

Proof

We join the points O and B with a line.

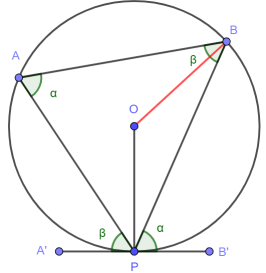
From the inscribed angle theorem we know that as we move A the ∠PAB remains constant and in fact equals ∠POB / 2. This holds even where A moves so that O is no longer inside ΔPAB.

As ∠POB = 2α, ∠OPB + ∠OBP = 180° - 2α. Since ΔPOB is isosceles ∠OBP = ∠OPB. So ∠OPB = 90° - α.

We also know that ∠B’PO = 90°. So ∠B’PB = ∠B’PO - ∠POB = 90° - (90° - α) = α = ∠PAB. ∎

The result for β is obtained in exactly the same way, joining O and A.

Where next?

We wrap up with two technical results. First up is the chord bisection theorem.