Circle theorems: Thales

1. Thales. The easiest circle theorem.
2. Inscribed angle. The angle subtending a major arc is constant.
3. Cyclic quadrilateral - opposite angles sum to 180°. Plus minor arc.
4. Tangent radius. Blindingly obvious, but a slippery proof.
5. Alternate segment. Perhaps the most unintuitive.
6. Chord bisection by radius. The relevant angle is 90°.
7. Equal length tangents. For completeness.

Thales's theorem is that the angle made between points A and B on the ends of a circle diameter and a third point P on the circle circumference is 90°.

Thales interactive

In the diagram below you can move point P on the circumference.

You can see that ∠APB is always 90°.

Thales: the proof

We first draw a line from O to P.

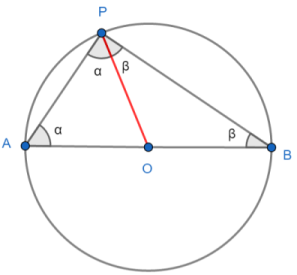
Now consider ΔOAP:

• |OP| = |OA| as both are radii.
• So ΔOAP is isosceles.
• Set the two identical angles to α.

Similarly ΔOBP is isosceles. Set its identical angles to β.

Sum ΔAPB angles: 180° = α + (α + β) + β which simplifies to α + β ∠APB = 90°. ∎

Where to now?

What if the chord AB is not a diameter? It turns out that ∠APB is still constant.

Many proofs are flawed: they consider only the simplest case. For more on this see the inscribed angle theorem.